Numerical Methods for ODEs#
Learning Objectives#
After reading this chapter the reader should know:
What constitutes an initial value problem (IVP)
Common methods and libraries for solving IVPs
Implicit and explicit equations
How to implement explicit and implicit ODE methods
Challenges and pitfalls that can be encountered in numerical simulations
Introduction#
The majority of the material presented in this chapter is based on Gros [Gro11]. The goal of this chapter is therefore to present the contents in a more practical manner. We’ll start by defining the initial value problem and common ways to solve ODEs in Python. We’ll then look at the theory behind numerical methods and its limitations.
Initial Value Problems (IVP)#
Throughout your studies you’ve encountered numerous ordinary differential equations (ODEs) of many shapes and orders. When we are solving ODEs given a set of initial conditions we are solving an initial value problem (IVP). It’s solution often yields equations which specify how a system changes over time. Formally, we can define an initial value problem as a function
where \(\Omega\) is an open set of \(\mathbb{R} \times \mathbb{R}^n\) together with a point in the domain \((t_0, y_0) \in \Omega\) called the initial condition. A solution to the initial value problem is a function \(y\) that solves the differential equation and satisfies \(y_0(t_0) = y_0\). We can express a higher order initial value problem by treating the derivative as an independent function, \(y''(t)=f(t,y(t),y'(t))\). In this manner we can represent an N-order differential equation as a set of N first order differential equations. An example of an initial value problem is the ordinary differential equation
We recognize the solution to this IVP as the solution \(x(t) = x_0\ e^{-at}\). We can show this in many ways, but how might we use python to solve this ODE algebraically?
We can use the SymPy method dsolve
import sympy as sm
sm.init_printing(use_latex='mathjax')
x = sm.Function('x')
a, t = sm.symbols('a t')
lhs = x(t).diff(t) + a*x(t) # Define left-hand side
result = sm.dsolve(lhs)
result
We can also specify the the initial conditions with the argument ics (initial conditions).
x0 = sm.symbols('x0')
result = sm.dsolve(lhs, ics={x(t).subs(t, 0): x0})
result
Exercise
Solve the differential equation \(\ddot{x} = -\dot{x} -x, \quad \dot{x}(0) = \frac{-x_0}{2}, \quad x(0) = x_0\) using SymPy.
Hint
You can use checkodesol to check your solution. See SymPy docs.
Solution
import sympy as sm
sm.init_printing(use_latex='mathjax')
x = sm.Function('x')
t, x0= sm.symbols('t x0')
lhs = sm.Derivative(x(t), t, 2) + x(t).diff(t) + x(t) # Define left-hand side
result = sm.dsolve(lhs, ics={x(t).diff(t).subs(t,0): -x0/2, x(t).subs(t, 0): x0})
result = result.simplify() #This is fine, but we can simplify it further
print(sm.checkodesol(lhs, result))
result
(True, 0)
For a more comprehensive tutorial on solving ODEs algebraically in SymPy, see the official documentation.
When working with complex models ODEs can become unpractical or even impossible to solve analytically. In that case we might want to use a numerical method to approximate a solution of the initial value problem.
For many practical applications a numerical approximation is often sufficient. A common solver often used in Python is the SciPy ODE solver solve_ivp.
Example: Solving ODEs with SciPy solve_ivp#
In this example we’ll demonstrate how to numerically solve the IVP \(\ddot{x} + 9x, \quad x(0) = 1, \quad \dot{x}(0) = 0\). You’re encouraged to code along. We first have to separate the second order ODE into two first order ODEs.
We can then define the system in python as a 2-dimensional first order ODE in system.
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
def system(t, X):
return [X[1], -9*X[0]]
Initial conditions are set as \(x(0) = 1\) and \(x'(0) = 0\):
x0 = [1, 0]
We specify the time span for the solution from 0 to 10 seconds:
t_span = (0, 10)
t_eval = np.linspace(0, 10, 100)
Solve the differential equation using SciPy’s solve_ivp:
solu = solve_ivp(system, t_span, x0, t_eval=t_eval)
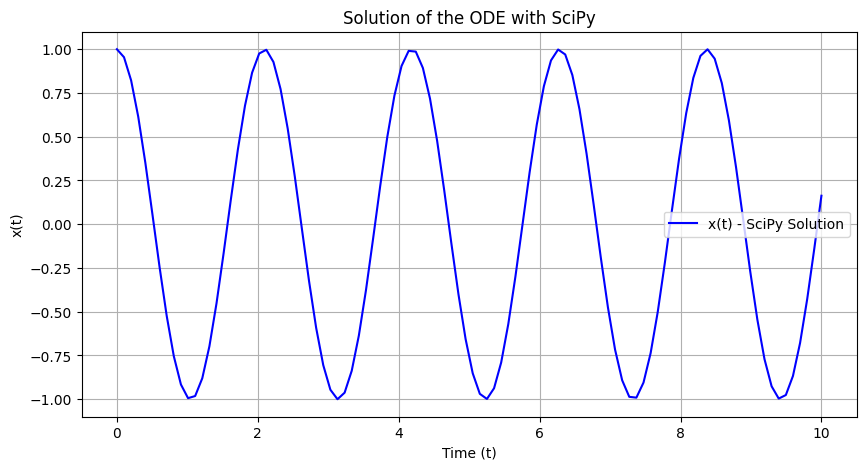
Plot the solution to visualize x(t):
plt.figure(figsize=(10, 5))
plt.plot(solu.t, solu.y[0], label='x(t) - SciPy Solution', color='blue')
plt.title('Solution of the ODE with SciPy')
plt.xlabel('Time (t)')
plt.ylabel('x(t)')
plt.legend()
plt.grid()
plt.show()
By solving this algebraically with SymPy we can examine the error:
z = sm.Function('z')
k = sm.symbols('k')
lhs = sm.Derivative(z(k), k,2) + 9*z(k)
result = sm.dsolve(lhs, ics={z(k).diff(k).subs(k, 0): x0[1], z(k).subs(k, 0): x0[0]})
result
We can then calculate the error and plot it:
algebraic_solution_func = sm.lambdify(k, result.rhs, 'numpy')
algebraic_solution = algebraic_solution_func(solu.t)
error = solu.y[0] - algebraic_solution
plt.figure(figsize=(10, 5))
plt.plot(solu.t, error, label='e(t) - SciPy Solution Error', color='blue')
plt.title('Solution error of the ODE with SciPy')
plt.xlabel('Time (t)')
plt.ylabel('e(t)')
plt.legend()
plt.grid()
plt.show()
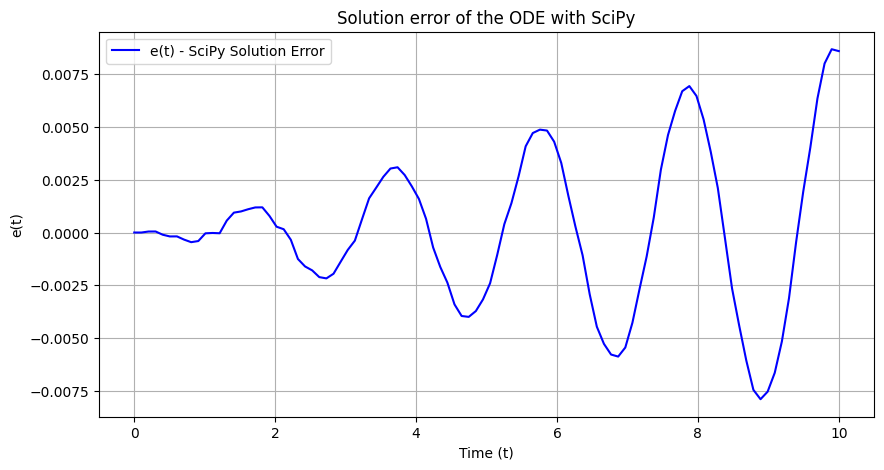
Although the error is quite small, we can see that it’s steadily grows as the integration errors accumulates. In the next sections we’ll look at how numerical methods are implemented and their limitations. We’ll start by looking at Euler’s method.
Exercise
Simulate the 2-dimensional system of equations \(t \in [0, 10]\) using SciPy solve_ivp.
Explicit Euler (ERK)#
The explicit Euler method, also called the forward Euler method, is really the simplest numerical scheme there is. We need two ingredients, the initial value problem we defined earlier and the definition of the derivative:
Armed with these two, we can first say that a good approximation to the derivative \(\dot{x}\) is the finite difference
This is a first order approximation to the derivative, which means that the explicit Euler method is a first order method. If we wanted higher order methods, we could design (and you will do this in the assignments) schemes that are higher order approximations to the derivative. But, at any rate, we need to relate this to the function \(f(t, x)\) if we are going to be able to solve it. In this context, the forward Euler method is defined as:
With some algebra, this can be worked into the form:
This gives a rule as to how we update the next step \(x_{n+1}\) using what we already know, namely the current step \(x_n\) and the time. If we apply this method to the model problem \(\dot{x} = \lambda x\), we get that
This model problem has the familiar solution \(x_0 e^{\lambda t}\) for some initial condition \(x_0\) and is not all that interesting in itself. However, this is a simple problem we can use to test the stability of numerical methods, which we also work with in the assignment on numerical solution. In the next section we will look at another method that looks very much like the forward Euler method, but is actually slightly different.
Implicit Euler (IRK)#
The implicit Euler method, or the backward Euler method, is a close cousin to the forward method. In fact, the only difference between the two is the index! Still using the same notation that \(\dot{x} = f(t, x)\) and that \(\dot{x} \approx \frac{x_{n+1} - x_n}{h}\), we define the backward Euler method as
The only difference is that the next step \(x_{n+1}\) features inside the function defining the system dynamics. In the case of the model problem, this is no issue, since we get that
However, this becomes much more complicated if the system dynamics is a vector valued function that may depend on the state \(x_{n+1}\) non-linearly. In general, we’re stuck with the formulation in (73). We would be able to find the next step only if we already had it, which means that for implicit methods we need additional steps to evaluate them. We’ll discuss this in the section below.
Implicit equations#
By implicit equation, we mean an equation that describes a relationship, but where the symbols cannot be rearranged to isolate the unknown quantity. This ties together with the last section where we found an equation where the unknown quantity \(x_{n+1}\) featured in an expression that may not have a known inverse. Initially, we’re stuck with the equation on the form
This equation is on a form known as a fixed point formulation, where the defining feature is that if we input the exactly correct \(x_{n+1}\) into the right-hand side, we get that same value back on the left-hand side. This is good news, as there are many methods to find the solutions to such problems (the so-called fixed points)!
Fixed point methods#
The general form of such problems are
Fixed point problems
Given a function \(G(x)\), find a point \(x^*\) such that
If we take \(x_n\) and \(t_{n+1}\) as constants for our problem above, we get a problem of this kind if we say that \(x^* = x_{n+1}\). At least the mathematicians are happy with that formulation (probably). The iteration in this type of problem comes from the fact that in many cases, we can define the function \(G(x)\) in such a way that we can set up a chain of guesses to the solution, or that for a sufficient initial guess \(x_0\), we can prove that repeatedly applying \(G\) in the sense that
eventually reaches the (or rather a) fixed point solution \(x^*\). In this situation, we could write that
Root-finding problems#
A closely related method for finding solutions to (nonlinear) implicit equations is the method of root finding. In this type of approach, we try to identify the zero of a function. The general form here is
The name root-finding is motivated by polynomials, where we say that the zeros of a polynomial are its roots. Thus, in the literature, you may find such methods referred to as “root-finding”, even though they are concerned with the zeros of a function. Also, if we spend some time thinking, we can see that it is possible to turn a fixed point problem into a root-finding problem. If we set \(F(x) = x - G(x)\), we obtain that a fixed point \(x^*\) of \(G\) is also a root (or zero point) of \(F\)! It is also possible to go the other way and converting a root-finding problem into a fixed point problem. The quickest way to go about it may be to add the input \(x\) to both sides. However, this does not always result in a fixed point formulation which lends itself well to iteration.
Newton’s method#
Newton’s method is one of several methods one can use to find the zero points of a function. Some good sources describing the method in greater detail can be found in LibreTexts [Ope16] or Wikipedia [Wik25a].
The main idea of the method is to use the tangent line as an approximation to the function in question, so that we can successively find better guesses to the root. For a function \(f(x)\), we can use the derivative of the function \(f'(x)\) to set up the following fixed point scheme:
As long as \(f'(x_n) \neq 0\) and the initial guess \(x_0\) is not too far off, this method will usually converge within some margin. By rearranging the expression slightly, we can say that the update to the point \(\Delta x_{n+1}\) is equal to
The reason we care about the “update” is because it gives us the iterative scheme were we simply compute the \(\Delta x_{n+1}\) with the \(x_n\) we currently hold as our best guess and then obtain a better guess by adding the update! Thus, the closer we are to a fixed point (i.e. our solution), the smaller the update will be. Since the scheme is iterative and will only give the right answer when we’ve done an infinite number of iterations, we have to be able to stop iterating when things are “good enough”. Since the update will get smaller and smaller, we can say that a good place to stop is when the update is smaller than a certain threshold, the error tolerance of the iteration. For a specific (user-defined) tolerance level \(\text{tol}\), we can say that if
then we accept the point \(x_{n+1}\) as a “good enough” solution. This is starting to sound like an algorithm we could implement for ourselves and use in potential implicit Runge-Kutta solvers. It’s been a while since we talked about those, but in the end, this is why we even need to discuss implicit equations and fixed points and all that.
At any rate, if we say that \(f(x_n)\) can be a vector-valued function (which often is the case in dynamical systems we care about), then the derivative will actually be the Jacobi matrix of the function, which we will call \(J_f\). In index-notation we have that
In this case, the division becomes multiplication by the inverse or that
While it’s not clear from the notation, bear in mind that the Jacobian may also be a function of \(x\), and so must be evaluated at the point \(x_n\). Now the time is right for writing the algorithm as a function in Python, and we might get something looking like the following:
def newtons_method(f, J_f, x_guess, TOL=1e-6, MAX_ITER = 100):
x = x_guess
for i in range(MAX_ITER):
delta_x = np.linalg.solve(J_f(x), -f(x))
x += delta_x
if np.linalg.norm(delta_x) < TOL:
break
return x, {"iterations": i, "delta": delta_x}
This function will return either when the update is sufficiently small or when the maximum number of iterations is reached. If we program a model problem to test this against, we can see whether it converges given our parameters.
def f(x):
return (x + 1)**3
def J_f(x):
return np.array([
[3 * (x[0] + 1)**2, 0, 0],
[0, 3 * (x[1] + 1)**2, 0],
[0, 0, 3 * (x[2] + 1)**2]])
zero_point, diagnostic_data = newtons_method(f, J_f, np.ones((3,)))
print(f"Zero point: {zero_point}\nNumber of iterations: {diagnostic_data['iterations']}\nDelta: {diagnostic_data['delta']}")
Zero point: [-0.99999908 -0.99999908 -0.99999908]
Number of iterations: 35
Delta: [-4.57840992e-07 -4.57840992e-07 -4.57840992e-07]
The code shows that the root of the function occurs when \(x = y = z = -1\). It also reached the root using fewer than the allocated iterations and with a final update within the accepted level of tolerance.
Example: Implicit Euler for a scalar system#
In this example we will implement some Python code for simulating the solution to an initial value problem based on a scalar function using the implicit Euler method. In the assignments you will need to solve systems where the dynamics are a vector-valued function and the Jacobian (needed for Newton iterations) is a matrix. In the scalar case, however, this is a bit simpler, both the dynamics function and the derivative are scalar functions. Hopefully, this allows you to see the general shape of the simulation code and realize what steps are needed along the way to make a fully functioning simulation code. Let’s dive in.
We will try to simulate the system defined by the ODE:
This will mean that the Jacobian of the system dynamics is
As code, these functions will look like
def system_dynamics(t, x):
return np.exp(-x**2)
def system_jacobian(t, x):
return -2*x * np.exp(-x**2)
By putting the expression for \(f(t,x)\) into the general implicit Euler method in (73), we get
We see that it will not be as simple to find a solution for this as it was for the model equation \(\dot{x}=\lambda x\), where we could find a solution using some algebra. Instead, we turn to solving the implicit equation using an iterative method. We choose Newton’s method, and in order to not confuse this example with previous code, we implement a scalar variant of the method (for variation, we use a while-loop):
def newtons_method_scalar(f, dfdx, x0: float, TOL=1e-6, MAX_ITER=100):
x, dx = x0, np.inf
i = 0
while np.abs(dx) > TOL and i < MAX_ITER:
dx = - f(x) / dfdx(x)
x += dx
i += 1 # important to update so that iterations are recorded
return x
As we’ve discussed earlier, the Newton’s method finds the roots of a function. If we want to find the next step, we have to construct a function that has a root precisely where the next step is! We can rearrange the implicit Euler method:
This means that the function we will try to find the roots of is:
Note that \(x_n\), \(h\) and \(t_{n+1}\) are parameters to the function that will change at each timestep, but still be known at each timestep. The only unknown quantity is \(x\), and if we put \(x = x_{n+1}\), we should get zero (by the construction of the function). We sometimes call this function the residual function since it is “what remains to be accounted for”, in a certain sense. If the residual is zero, our guess for \(x_{n+1}\) is correct, and while the residual is not zero, we continue guessing until we get it right. Due to the construction of Newton’s method, this is the function we have to give it, along with the Jacobian of this function. Crucially, it is not system_dynamics and system_jacobian that go into the Newton iterations, but the residual function and jacobian of the residual. The Jacobian of the residual is the derivative in the scalar case, so
One way of programming the two is:
def make_residual_function(f, dfdx, x_current, step_size, t_current):
def residual(x):
return x - x_current - step_size * f(t_current, x)
def residual_jacobian(x):
return 1 - step_size * dfdx(t_current, x)
return residual, residual_jacobian
Now, we are ready to put the parts together in a main simulation loop
t0, x0 = 0, 0.1
ts, xs = [t0], [x0]
t_end, h = 1, 1/100
num_timesteps = int(t_end / h)
for i in range(num_timesteps):
res, res_jac = make_residual_function(system_dynamics, system_jacobian, xs[i], h, ts[i])
x_next = newtons_method_scalar(res, res_jac, xs[i])
xs.append(x_next)
ts.append(ts[i] + h)
ts_fnc, xs_fnc = ts, xs # set aside for plotting later
From the code itself, it is really not possible to see that we use an implicit Euler solver. This is because the numerical scheme we use is baked into the definition of the residual. If we wanted to make it more clear, we could put it in the main loop. This might look like
t0, x0 = 0, 0.1
ts, xs = [t0], [x0]
t_end, h = 1, 1/100
num_timesteps = int(t_end / h)
for i in range(num_timesteps):
res = lambda x: x - xs[i] - h * system_dynamics(ts[i], x)
res_jac = lambda x: 1 - h * system_jacobian(ts[i], x)
x_next = newtons_method_scalar(res, res_jac, xs[i])
xs.append(x_next)
ts.append(ts[i] + h)
ts_inline, xs_inline = ts, xs # set aside for plotting later
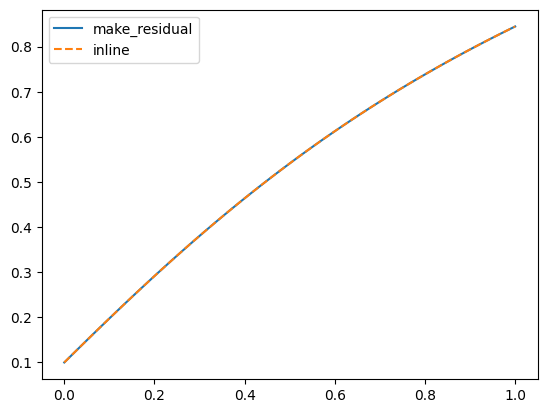
We can visually inspect that they do more or less the same by plotting them both.
plt.plot(ts_fnc, xs_fnc, label="make_residual")
plt.plot(ts_inline, xs_inline, label="inline", linestyle="--")
plt.legend(); plt.show()